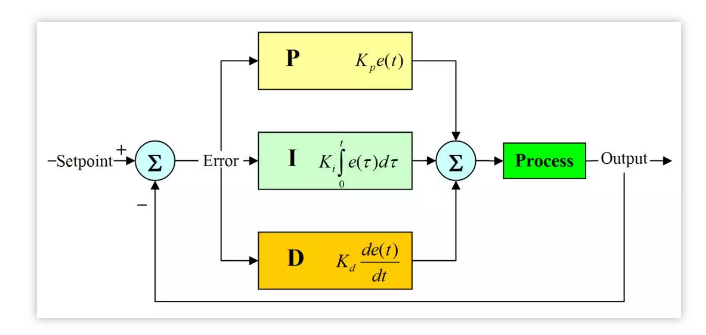
PID算(suàn)法可(kě)以說是在自動控制原理(lǐ)中比較經典的(de)一套算(suàn)法，在現實生活中應用(yòng)的(de)比較廣泛。

大(dà)學參加過電子競賽的(de)朋友都應該玩過電機（或者說循迹小車），我們要控制電機按照(zhào)設定的(de)速度運轉，PID控制在其中起到了(le)關鍵的(de)作用(yòng)。

說來(lái)慚愧，大(dà)學這(zhè)門課程學的(de)不咋滴，老師講的(de)課基本沒聽(tīng)進去過。直到後面接觸競賽，算(suàn)是對(duì)PID有了(le)很基礎的(de)一點點認識，直到現在工作實際應用(yòng)的(de)比較廣泛才知道它的(de)重要性。所以，這(zhè)裏特地回顧一下(xià)。

PID，即比例Proportion、積分(fēn)Integral和(hé)微分(fēn)Derivative三個(gè)單詞的(de)縮寫。

閉環自動控制技術是基于反饋的(de)概念以減少不确定性，在閉環自動控制原理(lǐ)中，我們把它叫做(zuò)“PID控制器”，拿控制電機來(lái)說，參考下(xià)面模型：

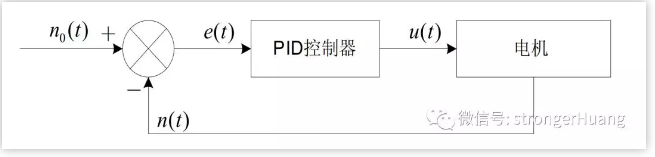
下(xià)面引用(yòng)一段網上經典的(de)話(huà)：

在工業應用(yòng)中PID及其衍生算(suàn)法是應用(yòng)最廣泛的(de)算(suàn)法之一，是當之無愧的(de)萬能算(suàn)法，如果能夠熟練掌握PID算(suàn)法的(de)設計與實現過程，對(duì)于一般的(de)研發人(rén)員(yuán)來(lái)講，應該是足夠應對(duì)一般研發問題了(le)，而難能可(kě)貴的(de)是，在我所接觸的(de)控制算(suàn)法當中，PID控制算(suàn)法又是最簡單，最能體現反饋思想的(de)控制算(suàn)法，可(kě)謂經典中的(de)經典。經典的(de)未必是複雜(zá)的(de)，經典的(de)東西常常是簡單的(de)，而且是最簡單的(de)，想想牛頓的(de)力學三大(dà)定律吧，想想愛(ài)因斯坦的(de)質能方程吧，何等的(de)簡單！簡單的(de)不是原始的(de)，簡單的(de)也(yě)不是落後的(de)，簡單到了(le)美(měi)的(de)程度。

常規的(de)模拟 PID 控制系統原理(lǐ)框圖如下(xià)：

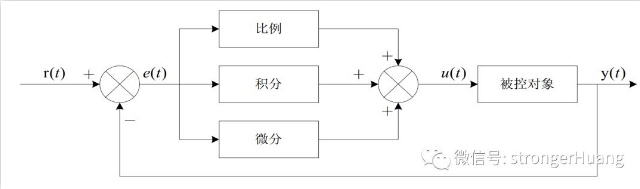
該系統由模拟 PID 控制器和(hé)被控對(duì)象組成。

上面框圖中， r(t) 是給定值， y(t) 是系統的(de)實際輸出值，給定值與實際輸出值構成控制偏差e(t) = r(t) − y(t).

e(t) 作爲 PID 控制的(de)輸入， u(t)作爲 PID 控制器的(de)輸出和(hé)被控對(duì)象的(de)輸入。 所以模拟 PID 控制器的(de)控制規律爲:

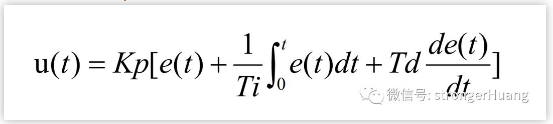
三個(gè)重要的(de)參數：

Kp：控制器的(de)比例系數.

Ti：控制器的(de)積分(fēn)時(shí)間，也(yě)稱積分(fēn)系數.

Td：控制器的(de)微分(fēn)時(shí)間，也(yě)稱微分(fēn)系數.

1、P - 比例部分(fēn)

比例環節的(de)作用(yòng)是對(duì)偏差瞬間作出反應。偏差一旦産生控制器立即産生控制作用(yòng)， 使控制量向減少偏差的(de)方向變化(huà)。 控制作用(yòng)的(de)強弱取決于比例系數Kp， 比例系數Kp越大(dà)，控制作用(yòng)越強， 則過渡過程越快(kuài)， 控制過程的(de)靜态偏差也(yě)就越小； 但是Kp越大(dà)，也(yě)越容易産生振蕩， 破壞系統的(de)穩定性。 故而， 比例系數Kp選擇必須恰當， 才能過渡時(shí)間少， 靜差小而又穩定的(de)效果。

2、I  - 積分(fēn)部分(fēn)

從積分(fēn)部分(fēn)的(de)數學表達式可(kě)以知道， 隻要存在偏差， 則它的(de)控制作用(yòng)就不斷的(de)增加； 隻有在偏差e(t)＝0時(shí)， 它的(de)積分(fēn)才能是一個(gè)常數，控制作用(yòng)才是一個(gè)不會增加的(de)常數。 可(kě)見，積分(fēn)部分(fēn)可(kě)以消除系統的(de)偏差。

積分(fēn)環節的(de)調節作用(yòng)雖然會消除靜态誤差，但也(yě)會降低系統的(de)響應速度，增加系統的(de)超調量。積分(fēn)常數Ti越大(dà)，積分(fēn)的(de)積累作用(yòng)越弱，這(zhè)時(shí)系統在過渡時(shí)不會産生振蕩； 但是增大(dà)積分(fēn)常數Ti會減慢(màn)靜态誤差的(de)消除過程，消除偏差所需的(de)時(shí)間也(yě)較長(cháng)， 但可(kě)以減少超調量，提高(gāo)系統的(de)穩定性。

當 Ti 較小時(shí)， 則積分(fēn)的(de)作用(yòng)較強，這(zhè)時(shí)系統過渡時(shí)間中有可(kě)能産生振蕩，不過消除偏差所需的(de)時(shí)間較短。所以必須根據實際控制的(de)具體要求來(lái)确定Ti 。

3、D - 微分(fēn)部分(fēn)

實際的(de)控制系統除了(le)希望消除靜态誤差外，還(hái)要求加快(kuài)調節過程。在偏差出現的(de)瞬間，或在偏差變化(huà)的(de)瞬間， 不但要對(duì)偏差量做(zuò)出立即響應（比例環節的(de)作用(yòng)）， 而且要根據偏差的(de)變化(huà)趨勢預先給出适當的(de)糾正。爲了(le)實現這(zhè)一作用(yòng)，可(kě)在 PI 控制器的(de)基礎上加入微分(fēn)環節，形成 PID 控制器。

微分(fēn)環節的(de)作用(yòng)使阻止偏差的(de)變化(huà)。它是根據偏差的(de)變化(huà)趨勢（變化(huà)速度）進行控制。偏差變化(huà)的(de)越快(kuài)，微分(fēn)控制器的(de)輸出就越大(dà)，并能在偏差值變大(dà)之前進行修正。微分(fēn)作用(yòng)的(de)引入， 将有助于減小超調量， 克服振蕩， 使系統趨于穩定， 特别對(duì)髙階系統非常有利， 它加快(kuài)了(le)系統的(de)跟蹤速度。但微分(fēn)的(de)作用(yòng)對(duì)輸入信号的(de)噪聲很敏感，對(duì)那些噪聲較大(dà)的(de)系統一般不用(yòng)微分(fēn)， 或在微分(fēn)起作用(yòng)之前先對(duì)輸入信号進行濾波。

 PID 控制算(suàn)法可(kě)以分(fēn)爲位置式 PID 和(hé)增量式 PID 控制算(suàn)法。

兩者的(de)區(qū)别：

（1）位置式PID控制的(de)輸出與整個(gè)過去的(de)狀态有關，用(yòng)到了(le)誤差的(de)累加值;而增量式PID的(de)輸出隻與當前拍(pāi)和(hé)前兩拍(pāi)的(de)誤差有關，因此位置式PID控制的(de)累積誤差相對(duì)更大(dà);

（2）增量式PID控制輸出的(de)是控制量增量，并無積分(fēn)作用(yòng)，因此該方法适用(yòng)于執行機構帶積分(fēn)部件的(de)對(duì)象，如步進電機等，而位置式PID适用(yòng)于執行機構不帶積分(fēn)部件的(de)對(duì)象，如電液伺服閥。

（3）由于增量式PID輸出的(de)是控制量增量，如果計算(suàn)機出現故障，誤動作影(yǐng)響較小，而執行機構本身有記憶功能，可(kě)仍保持原位，不會嚴重影(yǐng)響系統的(de)工作，而位置式的(de)輸出直接對(duì)應對(duì)象的(de)輸出，因此對(duì)系統影(yǐng)響較大(dà)。

下(xià)面給出公式直接體現的(de)C語言源代碼（請結合項目修改源代碼）：

1.位置式PID

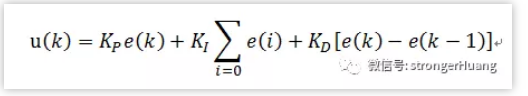
typedef struct
{
  float Kp;                       //比例系數Proportional
  float Ki;                       //積分(fēn)系數Integral
  float Kd;                       //微分(fēn)系數Derivative

  float Ek;                       //當前誤差
  float Ek1;                      //前一次誤差 e(k-1)
  float Ek2;                      //再前一次誤差 e(k-2)
  float LocSum;                   //累計積分(fēn)位置
}PID_LocTypeDef;

/************************************************
函數名稱 ： PID_Loc
功    能 ： PID位置(Location)計算(suàn)
參    數 ： SetValue ------ 設置值(期望值)
            ActualValue --- 實際值(反饋值)
            PID ----------- PID數據結構
返 回 值 ： PIDLoc -------- PID位置
作    者 ： strongerHuang
*************************************************/
float PID_Loc(float SetValue, float ActualValue, PID_LocTypeDef *PID)
{
  float PIDLoc;                                  //位置

  PID->Ek = SetValue - ActualValue;
  PID->LocSum += PID->Ek;                         //累計誤差

  PIDLoc = PID->Kp * PID->Ek + (PID->Ki * PID->LocSum) + PID->Kd * (PID->Ek1 - PID->Ek);

  PID->Ek1 = PID->Ek;  return PIDLoc;
}

2.增量式PID

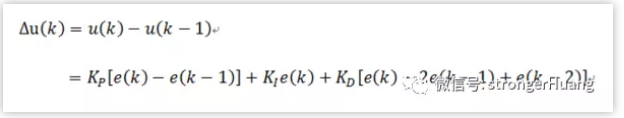
typedef struct
{
  float Kp;                       //比例系數Proportional
  float Ki;                       //積分(fēn)系數Integral
  float Kd;                       //微分(fēn)系數Derivative

  float Ek;                       //當前誤差
  float Ek1;                      //前一次誤差 e(k-1)
  float Ek2;                      //再前一次誤差 e(k-2)
}PID_IncTypeDef;

/************************************************
函數名稱 ： PID_Inc
功    能 ： PID增量(Increment)計算(suàn)
參    數 ： SetValue ------ 設置值(期望值)
            ActualValue --- 實際值(反饋值)
            PID ----------- PID數據結構
返 回 值 ： PIDInc -------- 本次PID增量(+/-)
作    者 ： strongerHuang
*************************************************/
float PID_Inc(float SetValue, float ActualValue, PID_IncTypeDef *PID)
{
  float PIDInc;                                  //增量

  PID->Ek = SetValue - ActualValue;
  PIDInc = (PID->Kp * PID->Ek) - (PID->Ki * PID->Ek1) + (PID->Kd * PID->Ek2);

  PID->Ek2 = PID->Ek1;
  PID->Ek1 = PID->Ek;  return PIDInc;
}